Your Ultimate Guide To The Circle Theorem

We all are familiar with a circle and its various properties. To get an in-depth mathematical understanding of the shape, we must learn all its distinctive properties. A circle is often defined as a shape with each point equidistant from its centre. The centre is denoted as 'o', and all the equidistant points from the centre points together are called the circle's circumference.

The term circle derives from the Greek word 'krikos' translated to ring in English.

Circle theorem refers to the various circle theorems taught in the senior secondary certificate course. It includes the concepts of a sector, tangent, secant, and various degrees of angles. The circle's centre is a fixed point from where each point on the circumference is equidistantly called the radius or radii. These theorems are concerned with angels formed at the centre, semicircle, sector and the angels of a cyclic quadrilateral.

This blog will discuss eight circle theorems and learn their applications with some real-life examples.

What Are the Eight Circle Theorems?

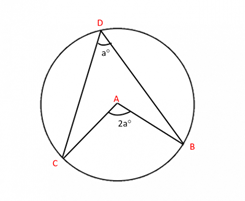
Theorem 1: The angle formed by an arc at the centre is double the angle at any circumference point.

Angle formed at the centre of a circle measures twice the angle formed at any other point on the circumference; if the angle formed at the circumference is 30 degrees, then the angle at the centre will be 60 degrees. Also known as the inscribed angle theorem can also be understood as angles on the same arc are equal and measure half the angle formed by the same arc at the circle’s origin.

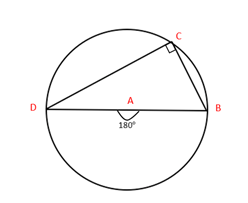
Theorem 2: Angle at the semicircle is a right angle.

The angle formed on the semicircle to the circumference is a right angle. Also known as Thales's theorem, if B, C, and D are three distinct points on the circumference of a circle and BD is the diameter, the angle BCD is a right angle.

Theorem 3: Angels formed on the same segment are equal.

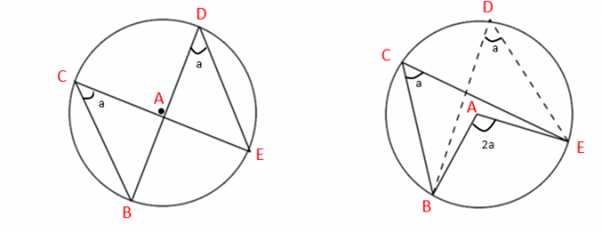
The angles formed on the same segment are equal. It can also be proven using the inscribed angle theorem; the angles on the circumference are equal to half of the angle projected at the centre of the circle on the same segment and hence are equal to each other.

Archimedes's circle principle proves that the area inscribed inside a circle is similar to the area of a triangle that has an equal base length to the circle's circumference and height equal to the radius.

Theorem 4: Adding the opposite angles of cyclic quadrilateral results in 180 degrees.

 A cyclic quadrilateral is inscribed inside a circle; all four corners of the circle are on the circle's circumference or inside the circle.

 According to the angle sum theorem, the sum of all four angles of a quadrilateral is equal to 360o. Therefore, the theorem is also true for a cyclic quadrilateral.

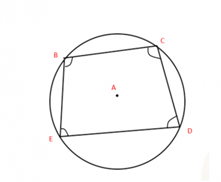
This can be proven using the Thales theorem, the angle formed on a semicircle is 90^o, if EC is diameter then angle B and angle D is 90^o each and hence the sum of opposite angles is 180^o.

Theorem 5: The length of two tangents from a point outside the circle to the circle is equal.

Tangent EC and AD are of the same length, from a point on the circle (D,E) to a point outside the circle (C) are equal.

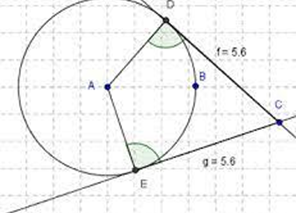
 According to the theorem, DC is EC.

Theorem 6: The angle between two tangents and the radius of a circle is a right angle.

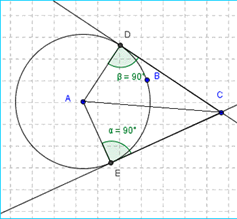
The angles formed between the radius and the tangent to a circle are the right angles. We can prove this theorem using the circle theorem 5. According to the alternate segment theorem angle, DAC is equal to ECA, which is true for EAC and DCA. Hence the sum of DAC + EAC is equal to DCA + ACE, resulting in angel A = angle C.

The same theorem proves angle D = angle, all the angles of a quadrilateral are 90 degrees. There we can conclude that Theorem 6 is true.

Theorem 7: The angle formed by a tangent and a chord of the circle is equal to the angle formed in the alternate segment and the tangent.

It is also known as the alternate segment theorem, it states that the angle between a tangent on the circle’s circumference and chord inside the circle measures equals the angle in the alternating segment.

 According to the theorem angel, FED = angle FDC. Hypothetically, if lines BC and FD are extended, BC is parallel to FD and ED is the transversal, angle FED and angle FDC are alternate angles and hence are equal.

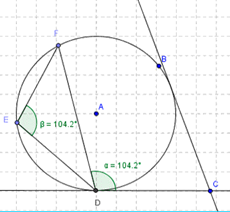
Theorem 8: The perpendicular from the origin of a circle to a chord divides it into two.

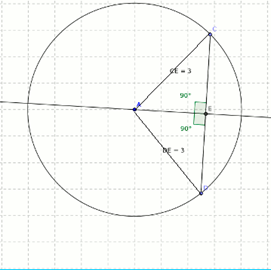
Here AC = AD as both are radii of the circle, and angles opposite to equal sides are equal (according to Euclid's postulates); hence angle ACE = angle ADE, AE is the common line segment that both triangle AED and triangle AEC share. Using similar triangles rule ASA, triangles AED and AEC are similar and equal, hence ED = EC.

These eight theorems are the most prominently used theorems concerning the properties of a circle and are often utilised in various real-life circumstances. We'll see some real life applications of these theorems in the next section of this blog.

Real-life applications of circle theorem

A circular shape can be commonly seen; in fact, we are surrounded by circular objects. The difference between a three-dimensional and a two-dimensional shape is the principles used for understanding the uses and applications. A cylinder is a 3-D object, but it has a face that is circular, similar to this, a wall clock, a wheel, a doorknob, and many other real-life objects use the principles of a circle.

A photographer uses the circle theorem to adjust the lens of their camera. The radius of the lens is used for determining its focal length. The aperture of the camera lens depends on the diameter of the lens. The angle of incidence of the light and the exposure of the object to the light is very important for taking the perfect picture, and the lens plays a key role in it.

Euclid's book of Elements states all the properties of a circle and cyclic quadrilateral, dating back to 650BC.

The navigation system of an aeroplane or ship uses the circle theorem to calculate the distance of the approaching object. The distance from the origin and destination point is also calculated using the circle theorems. The navigation map of aeroplanes and ships are shaped as 2-D circles following the destination signals displayed as a dot on the screen. Hence the calculation of distance and time requires the use of the circle theorem and other variables like air, pressure, wind speed and direction.

The Thales theorem of circles is used to create art, and sculpting, any real-life circumstances requiring precision use this theorem. Sculptures use the circle theorem to develop accurately in their structures and design various circular objects like cups, vases, and bowls.

Click on the other live blogs to get expert insight on various academic topics and join the discussion among university students worldwide. Get high-quality assignment help at the My Assignment Services at affordable prices; enrol today!